Many people around the world enjoy looking at pictures of Loch Ness through the Scotland-Online webcam installed at Temple Pier, Drumnadrochit. People sometimes see things they cannot identify, and this page is designed to help them calculate the distance away of any object, and also it's size.
The method shown involves only the most basic trigonometry based on right-angled triangles - the sort of thing school pupils are taught from the age of about 11 years. If you want a qualified teacher go see Dave. If you can put up with me, read on.
Here is a nifty map of the area where you can zoom in and out and move around and explore the area. You could print out the area of interest and turn the sheet round - it is much easier than trying to turn your monitor (or your head) upside down!
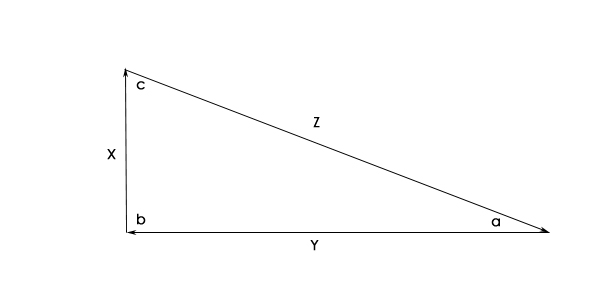
The Basics - The Amazing Right-Angled Triangle
This triangle, like most, has three sides and three corners or angles joining them together. These are the basic features:
the angles a, b and c add up to a toal of 180° (degrees)
b is always 90°, so the other two add up to 90° between them
the side Z opposite the 90° or "right-angle" is called
the hypotenuse and features in the well-known saying "the square on the hypotenuse
is equal to the sum of the squares on the other two sides". So if X=3, and
Y=4, then Z² = 3² + 4² = 9 +16, =25
so Z = the "square root" of 25, which is 5.
It gets even cleverer because you can find out everything about the triangle if you know the length of one side, and one angle (in addition to the right angle) using the basic trigonometrical formulae for sines, cosines and tangents as they are called.
We'll go over these by means of simple examples.
The "sine" of an angle (written as "sin") is given by the length of the opposite side (that's the side opposite the angle we're interested in)divided by the length of the hypotenuse, so "sin a" in the diagram above is X / Z. When we put the numerical values in for X and Z, we get sin a = 3 / 5 = 0.6
If you have a scientific calculator, or can steal one off your
kids / old folk, you can find out what angle a really is. Just enter "0.6
INV sin" and the machine, after careful thought, will
display 36.86989765 degrees. (Remember the formula by s=o/h....soh)
(After hours of surfing I found one right under my nose in Windows 98
- at Start > Programs > Accessories > Calculator and click on "View"
to select "Scientific".)
The "cosine" of an angle (written as "cos") is given by the adjacent side (that's the side next to it which isn't the hypotenuse) divided by the hypotenuse, so cos a = y / z, or 4/5=0.8 in the example above. Grab that calculator again and enter "0.8 INV cos" and it will say, remarkably, 36.86989765 degrees. (Remember the formula by c=a/h ....cah)
That only leaves (for now!) the "tangent" of an angle, which is the
opposite side divided by the adjacent side, so tan a in the
example above is given by x / y or 3 / 4 and is therefore 0.75. Get
the calculator and enter 0.75 INV tan and, well you know what to expect.
Yup, 36.86989765° (Remember the formula
by t=o / a ...toa)
So when trying to "solve" these triangle problems, you choose the formula which fits in with what you know already...if you know the opposite and adjacent sides to your unknown angle, use the "tan" formula t=o/a and so on.
If you know the angle in degrees and want to find the "tan" enter
the number of degrees (e.g. 36.9) then press "tan". If you know the "tan"
and want to convert it to actual degrees, enter tan value (e.g. 0.75) then
INV then tan. If you can't lay hands of a scientific calculator, borrow
Rolf's.
In order to measure something - anything - you have to compare it
with something you know the size of. If the thing you are measuring is a
small piece of wood, you lay a rule or measuring tape alongside it and compare
the two to learn how long the wood is. In the case of web cam pictures we
need fixed objects of known size, and we will find these around the shoreline.
In addition, when we measure things we can either measure them in units of
length (metres) or in units of angle (degrees). The angular measure is useful
if we don't yet know how far away an object is...a golf ball at arms length
and the Moon 240,000 miles away are both about 0.5 degrees in angular
dimension.
That's the (first) boring bit over with - let's see what this means with a real web cam. Before we could start, I had to do some some careful research using a Global Positional System receiver from a couple of boats to accurately plot the positions of various points around Urquhart Bay, in addition to getting accurate dimensions for the heights and widths of various buildings.
I have calculated that the distance from the web cam to the castle tower is 1440 m, and I am reliably informed that the width of the castle tower as viewed from the web-cam is 12.5 metres. Let's make a diagram and work out the angular size of the castle tower which will be our "measuring rod" for pictures in this part of the bay.
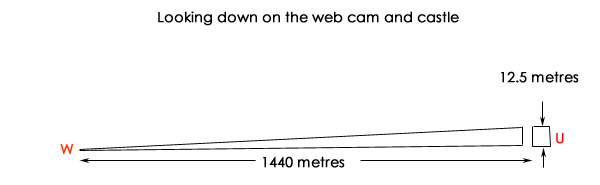
So what is the angular size of the castle when viewed from the web-cam? Piece of cake!
tan (angle of view) = opposite / adjacent, which = castle tower width / range to tower
= 12.5 / 1440, = 0.00868056
then enter "INV" then " tan" to get the answer = 0.497346705°
lets call it 0.5 degrees of arc.
So, from the webcam, the width of the castle tower is 0.5° This is measure # 1
Let's now use that to make another measure on
a real web-cam picture...

In the wider angle shots the castle tower isn't clearly visible, but the points at the castle and below Mrs Cary's house are, so they can be used for measuring. Since the width on the picture is 5.75 times the width of the castle tower, the angular distance between these two points is 5.75 x 0.5 = 2.875 degrees. This is measure #2
Finally, in this introduction, let us measure an artificial object first for distance, and then for size.

Artificial "Nessie"
The first step is to work out the distance to the object "N" as an angle. We know the castle tower is 0.5 degrees wide, so we can measure how much further down the picture our object is, relative to the "Castle Point" where the outcrop of rock juts out into the loch. If we try to measure it directly above the object "N" we could be mislead by shadows and poor light. If you are using a program like Adobe Photoshop you can superimpose a grid and even use built-in measuring devices, if not, you can measure off the screen or a print-out.

We will start by comparing the width of the tower as it appears in
the picture with the distance down the picture to the base of the "Nessie".
When I did this I got a width of tower of 43 pixels ( you can use whatever
units you choose) and a distance down to "N" of 32 pixels.
This means that "N" is 32 / 43 x 0.5 degrees lower down the picture than
the Castle Point. With the calculator this angle works out to be 0.37209 degrees.
(I know that this level of precision is quite unreasonable, but we
can round up the figures to a sensible number of decimal places at the end
of the job.)
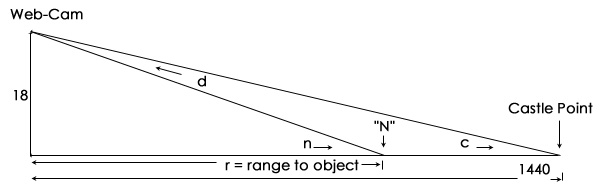
Let's work out the angle at "c" ...
tan c = "opposite over adjacent" or o ÷ a, = 18 ÷ 1440, =0.0125
so angle at c is ( 0.0125 INV tan...) 0.7161599 degrees.
We have just measured how much further down the object is: 0.37209 degrees, so we can add the two together to get the angle at "n". 0.7161599 + 0.37209 = 1.08825 degrees.
Nearly there now!
We know angle "n", the 18 is the same, so the range to the object can be worked out using the tan formula.
tan n = 18 / range "r"
and re-arranged, this becomes range "r" = 18 / tan n, = 18 / tan 1.08825 = 947.57 metres.
Because of the difficulty in accurately measuring the web-cam picture is would only be fair to claim that the object was "about 950 metres away."
What about the size of it ? Well, now we have a distance we can measure it's length as an angle, and covert it to a linear measure using the tan formula.
The length appears to be 12 pixels, and the tower width is 43 pixels, so the angular "length" dimension is 12 ÷ 43 x 0.5 degrees, = 0.13593 degrees.
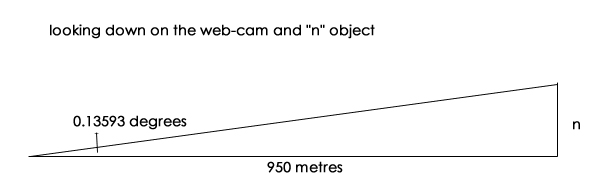
Nessie's length in this example is given by tan angle 0.13593 = n / 950 metres
so 0.0023724 = n / 950, so n = 0.0023724 x 950 = 2.25 metres.
You can go ahead and measure the height of its neck if you want to. In practice, the hardest part of the job is getting any kind of accurate measurement of the range to the object due to the fuzzy outlines of a web-cam image. This is made even more difficult when objects like boats have colours which blend with the water colour, and are of low contrast.
To measure objects in other parts of Urquhart Bay and Loch Ness covered by the web-cam but lacking the castle tower, we need other measured objects and ranges to them to base the calculations on.
These will be uploaded to this page in the near future, or you can work them out for yourself using an Ordnance Survey 1:50,000 map Sheet 26, "Inverness"...or go to the dynamic map mentioned at the top of the page.
Good Luck.
Correction and refinement to the information on this page is welcomed - send it to
![]()