Myths v Maths
One method used in examining the Bavister Photograph

Image Copyright © 2000 Loch Ness Project.
A part of the original image is reproduced here.

Image Copyright © 2000 Loch Ness Project.
A part of the original image is reproduced here.
Assuming for one moment that the object is really out there on the water, and not a bit of dirt on the film surface, is there any way of working out the size of the object in the photograph as a "desk study" as an alternative (or in addition) to visiting the site and sending out a boat into the middle of the loch?Well, I think there is. We only need to establish the exact location that the photograph was taken from, and fix it on a 1:50000 map of the area, and have a version of the original picture to refer to. This much has already been done, so from here on, anyone with a calculator can do the sums for themselves. The problem can be reduced to a few right angled triangles, and all we need to is to apply basic trigonometry.
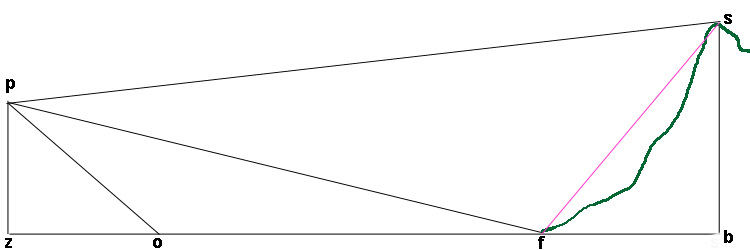
Diagram 1.
The Diagram.This is not drawn to scale, and the heights are exaggerated. Photographer p is at a height of pz above the loch surface. The mysterious object o is at some distance po away from the camera. Beyond o is the far shore at f, and above that the skyline at s.
Our first task is to work out the distance zo.
A careful study of the published picture has shown the most likely location it was taken from. Measuring from the Ordnance Survey map, I make pf to be 5500 metres, and ps to be 7500 metres. The height of the hill, if I have identified it correctly, is 440 metres above Ordnance Datum, and the surface of Loch Ness is about 15 metres above that, so sb * is 425 metres. By coincidence, the height of the road above the loch surface at p is believed to be 15 metres, and a photographer would normally hold a camera about 1.5 metres above ground level, so I am taking pz to be 16.5 metres. When this is rechecked, any corrections will be pointed out on this page. In some of the following calculations the positions p and z can be taken as being the same.
(* "Foul Play! I hear you shout ...you can't see sb, only sf, and that is not the same dimension!!! "
Er...O.K...yeah... you're right, I'm wrong.... so let's work it out:
sf ² = sb² + fb² = (425x425) +( 2000x2000) = 4,180,625
so sf = 2044.65 metres.Angle sfb is given by tan¯¹ sb / fb, = 425/2000 = 12 degrees, so visual length "seen" by camera at p is 2045 x cos 78, = 424.5 metres - only half a metre different from the assumed dimension!)
spb (~=szb) is given by tan spb = sb / zb, = 425 / 7500 = 0.05667, so sp(z)b = 3.243 degrees
We now know that a vertical distance of 425 metres at a distance of 7500 metres subtends an angle of 3.243 degrees and this is represented in the published picture by the visual height of the skyline above the loch shore. Measuring off the published image , this was 39.85 millimetres.
Now we are getting somewhere... we can measure a vertical height in the picture and convert it into a vertical angle.
The average distance of the "waterline" on the mystery object below the shoreline is 5.6mm on my screen, and this corresponds to the angle fpo, and is 5.6 / 39.85 x 3.243 = 0.4557 degrees.So now we have angle fpo.
If we now imagine ourselves at point f, looking back to p and z, the angle pfz is given by tan ¯¹ 16.5 / 5500 = 0.172 degrees.
pfz is a right-angled triangle, so angle fpz is 90- 0.172 = 89.828However, we have already calculated angle fpo to be 0.456, so angle zpo = 89.829 - 0.456 = 89.372 degrees
tan opz = oz / pz,
so oz = pz x tan opz, = 16.5 x (tan 89.372) = 1474 metres.
Repeat measurements gave slightly differing values, but the process can be repeated if I have a photographic print to work from.
Can we go any further?I think so.
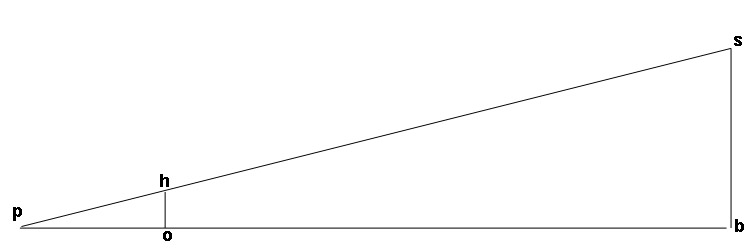
Diagram 2
Knowing the range of the object and the height and distance to the skyline, we can now scale off the actual linear dimensions as follows:
sb / bp = ho / op for any value of op.
Measurements of length of the object range between 0.237 and 0.247x ho, due to the difficulty of measuring the pixels.
Measurements of object height range between 0.063 and 0.070x ho.
So how big is this Nessie?
The calculations indicate that a probable visible length for an object at o is in the range 1474 / 7500 x 425 x 0.237 ( or 0.247 ) = 19.8 (or 20.6) metres, or 66 to 68 feet. Make a note of this!
In height, the object can be measured at between 0.038x and 0.044x the apparent height of the hill, which when adjusted for distance gives heights of between 3.16 and 3.69 m ( 10 to 12 feet) high at 1474 metres range.
The implication of these results is that some object about 70 feet long and 10 feet high out of the water was not seen by anyone at the the time, but nevertheless appeared on a photograph. If an animal, it would inevitably weigh several tens of tonnes.
Comparison with image of M.V.Deepscan.The length of the Loch Ness Project's research boat Deepscan ( although not at exactly the same range) can be scaled off from the photographic image as being 0.47x the mystery object, = 0.47x 20 metres, = 9.4 metres (30.8 feet). It is actually 32 feet long, so shows the calculations to be reasonably correct.
My conclusions:
These lengths and heights above water, arrived at by two quite independent methods, are remarkably consistent with each other, but barely consistent with a credible living creature. If they can be verified by some other means, I believe some other explanation should be sought.
Dick Raynor, 5th December 2000.
Further thoughts - 15th December 2000 There are not many vessels of such great size plying the Caledonian Canal, and it has already been possible to eliminate some of the converted barges, as they were known to be elsewhere at the time of the photograph. One, however, the "Scottish Highlander", remains a contender. Let's take another look at the overview.
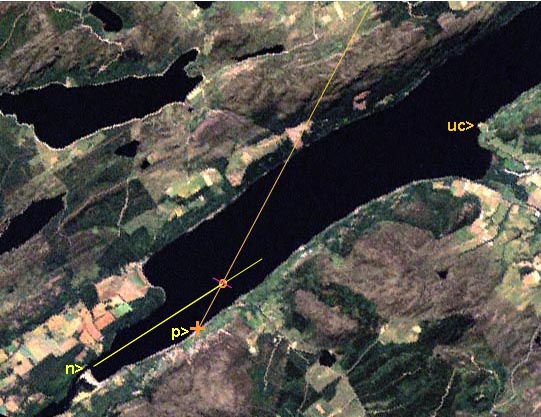
If our mystery picture really is a photo of a large commercial vessel steaming along Loch Ness, then we (at "p") will in all probability NOT be seeing it fully "side on", (shown in pink) as it will be heading to or from the place called "Bona Narrows", at "n", along the yellow line shown above. The angle we need to measure is angle nop. This is quite easily done and turns out to be 30 degrees, give or take a degree.
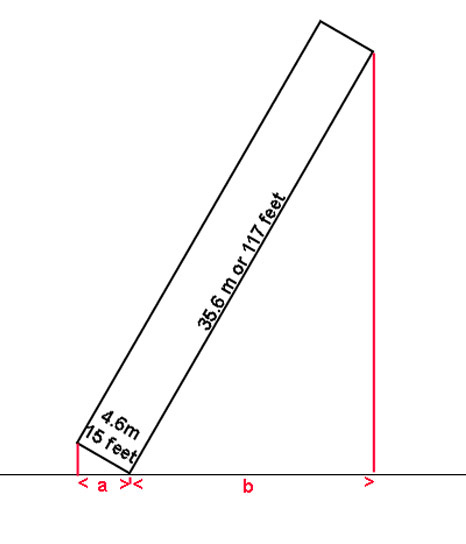
So how big is the "Scottish Highlander"? She is 35.6 m or 117 feet long and 4.6 m or 15 feet in the beam. A bit of geometry is all we need to work out the visible length, "a" plus "b".OK, the boat is not quite as brick-shaped as my diagram....but nearly.
We are seeing the bows at an angle of 30 degrees, and the length of the vessel at an angle of 60 degrees.
So, as the cosine of an angle in a right angled triangle is given by the adjacent over the hypotenuse, and the angle is 30 degrees, then cos 30=a / 15 ft, and so rearranging the equation,
a = cos 30 x 15 ft, a = 0.866 x 15 = 13 feet ( 3.96 m)Similarly, b = cos 60 x 117 ft , = 0.5 x 117 = 58.5 feet ( 17.82 m)
The visible length to an observer at a distance is then a + b, = 71.5 feet or 21.8 metres.
In view of the remarkable similarity between the size of the object in the photograph and the calculations above I suggest that the most likely object to show a visible length of about 70 feet to an observer or camera at the relevant location, time and date is the barge "M.V. Scottish Highlander" on course for Bona Narrows, and that the photograph which was said to have been taken on July 13th 2000 at about 11 a.m. shows this vessel.
In the light of these calculations and and other data presented, I believe that this photograph can be adequately explained without invoking the existence of any unknown large creature in Loch Ness.
It will however remain a picture of "Nessie" for many people. Nessie is something seen ( or, in this case photographed) for which the observer has no obvious explanation . My conclusions are, I believe, scientifically derived, but that does not guarantee that they are absolutely correct, and I would welcome discussion on the measurement techniques.
The objective of the investigator is to apply basic analytical techniques to all such evidence, in order to separate apparent wheat from apparent chaff, and focus on the deeper mysteries - and there are still plenty of them at Loch Ness.
To see how a barge might appear, take a look at the barge page
These calculations have been made possible by information supplied by Adrian Shine, Loch Ness Project, and original procedures impressed by Mr Cornelius and other Maths teachers at Scunthorpe Grammar School between 1960-65. Thank you all.